Back to Contents!
Next: Angular Momentum Up: Completing the Circle Previous: Rolling Motion cont'd.

Statics Problems

One of the most common application of torque and force diagrams is in the case of static objects. That is, we want to determine forces and positions where those forces act so as to guarantee that objects remain at rest with no turning or translational motion. The following are examples of "greatest hits" for statics problems.

  1. A ladder of weight 60 Nt leans against a frictionless wall. The other end of the ladder is on a floor where the coefficient of static friction is 0.3. If the bottom of the ladder is located 3 meters from the wall and the length of the ladder is 5 meters, find the magnitude and direction of all forces, other than the weight, acting on the ladder.

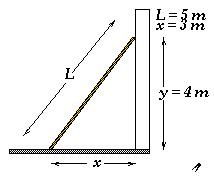
    Solution: The forces acting on the ladder come from gravity, static friction (the ladder is not moving), and contact with the floor and the wall. Since no friction is acting at the wall, only the normal force, Fw, is acting there. At the floor, the static friction magnitude is unknown because its value can be anywhere between 0 and the maximum possible value of musFN. We note that we have chosen the angle theta such that theta = arctan(3/4) = 37° and we have chosen the rotation axis for calculation of torques to be perpendicular to the plane of the page and passing through the point of contact between the ladder and the floor. Since we want the translational and angular accelerations to be zero, we need the net torque and net force to be zero, so

    and

    x: fs - Fw = 0 ==>
    fs = Fw
    y: FN - W = 0 ==>
    FN = W = 60 Nt
    T: Fw, pL - Wp(½ L) = 0 ==>
    Fwsin(theta) = ½ Wcos(theta) ==>
    Fw = ½ Wcot(theta)
    = ½ (60 Nt)cot(37° )
    Fw = 40 Nt

    From our x equation of motion, we have fs = Fw = 40 Nt.

  2. What is the maximum distance at which the bottom of the ladder in the problem above can be placed away from the wall before the ladder slips?

    Solution: All of our force diagrams will appear the same. The only things that have changed is that now x and y no longer equal 3 m and 4 m, respectively. However, it must still be true that (5 m)2 = x2 + y2. Also, we see that the frictional force does point to the right as we assumed in the force diagram for the previous problem, so the static frictional force will have to go to its maximum value, mus FN = (0.3)(60 Nt) = 18 Nt, to keep the ladder from slipping. From our x equation of motion, we have

    Fw, max = fs, max = 18 Nt

    To get the maximum distance of the bottom of the ladder from the wall, we use the torque equation from the previous problem to determine the maximum value of theta.

    Fw, max = ½ Wcot(thetamax) ==>
    thetamax = arccot[2Fw, max/ W]
    = arccot[2(18 Nt)/(60 Nt)] = 59°

    This maximum value of theta corresponds to a maximum distance from the wall as follows:

    L sin(thetamax) = xmax = (5 m)sin(59° ) = 4.3 m

  3. A beam with weight W1 is attached by to a wall by a hinge and rope that extends from the opposite end of the beam to the wall (see the figure below). A block of weight W2 hangs from the opposite end of the beam. If W1, W2, and theta are all known, find the magnitude and directions of all other forces acting on the beam.

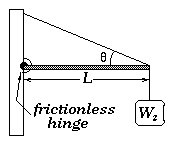
    Solution: We draw the free-body diagram depicting all the forces and torques acting.

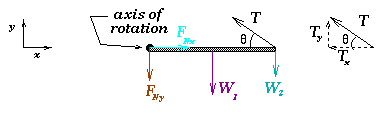
    The torques should be calculated around an axis perpendicular to the page and going through the connection between the hinge and the beam. This eliminates the need to find the torque due to the two unknown forces which the hinge provides on the beam. For static conditions, the net forces and torques must be zero, so

    x: FNx - T cos(theta) = 0 ==>
    FNx = T cos(theta)
    y: T sin(theta) - FNy - W1 - W2 = 0 ==>
    FNy = T sin(theta) - W1 - W2
    torque: (T sin(theta))L - W1(L/2) - W2L = 0 ==>
    T sin(theta) = ½ W1 + W2

    With T*sin(theta) known in terms of W1 and W2, we can find T as (½ W1 + W2)/sin(theta). We also have FNx = T cos(theta) = (½ W1 + W2)cot(theta) and

    FNy = T sin(theta) - W1 - W2 ==>
    FNy = -½ W1

    The minus sign indicates that we chose the wrong direction for FNy. This force actually points up rather than down. Keep in mind that the equations for force and torque will automatically indicate the correct directions for forces provide you are consistent in keeping track of signs.


    Next: Angular Momentum Up: Completing the Circle Previous: Rolling Motion cont'd.

    larryg@upenn5.hep.upenn.edu
    Thu Jan 29 17:38:58 EST 1998
    subsection4_1_5.html