|
Một người tiêu dùng có thu nhập I = 900 dùng để mua 2 sản phẩm X và Y với Px = 10đ/sp; Py =40đ/sp. Mức thỏa mãn được thể hiện qua hàm số TU =(X-2)*Y
Yêu cầu:
-
Viết phương trình đường ngân sách theo 3 dạng khác nhau
-
Viết phương trình hữu dụng biên cho hai loại hàng hóa
-
Tìm phối hợp tối ưu giữa hai loại hàng hóa và tính tổng hữu dụng tối đa đạt được
-
Nếu thu nhập tăng lên 1220, trong khi giá 2 hàng hóa không đổi, phối hợp tối ưu mới và tổng hữu dụng đạt được là bao nhiêu?
-
Nếu thu nhập giảm xuống còn 740, trong khi giá 2 hàng hóa không đổi, phối hợp tối ưu mới và tổng hữu dụng đạt được là bao nhiêu?
-
Mô tả các câu trên bằng đồ thị và vẽ đường tiêu dùng thu nhập dựa vào kết quả 3 câu từ 3-5.
-
Vẽ đường Engel mô tả mối quan hệ giữa thu nhập và cầu hàng hóa X và tính hệ số co giãn của cầu theo theo thu nhập trong 2 khoảng thu nhập: (1) từ 720 đến 900 và (2) từ 900 đến 1220.
Lời giải
Câu 1:
Người tiêu dùng có thu nhập 900 (I) để mua 2 hàng hóa nên số tiền này bằng tổng số tiền chi mua hàng hóa X (PX*X) cộng với tiền chi mua hàng hóa Y (PX*X), vậy phương trình đường ngân sách là:
10X +40Y = 900
ó X + 4Y = 90 (1)
Phương trình này có thể được viết lại dưới 2 dạng Y=f(X) và X=f(Y) bằng cách chuyển vế như sau:
X = -4Y +90 (2), hoặc
Y = -1/4X +45/2 (3)
Câu 2:
Từ lý thuyết ta biết được, hàm hữu dụng biên là đạo hàm của hàm tổng hữu dụng
ð MUX =(TU)x’ = Y
và MUY =(TU)Y’ = X-2
Câu 3:
Theo lý thuyết, phối hợp tối ưu giữa 2 hàng hóa đạt được khi thỏa mãn hệ phương trình:
I = Px*X + PY*Y (1) - PT đường ngân sách
và MUX*PY = MUY*PX (2) - PT tối ưu trong tiêu dùng
Thế các giá trị có được từ đề bài và kết quả câu trên vào, ta được
900 = 10*X + 40*Y (1’)
và Y*40 = (X-2)*10 (2’)
ó
90 = X + 4Y (1’’)
và 2 = X – 4Y (2’’)
Lấy (2’’) + (1’’)
=> 2 X = 92 ó X = 46
Thế vào (2’’) => Y = 11
Thế giá trị X, Y vào hàm tổng hữu dụng ta được
TU = (46 – 2)*11 = 484 (đơn vị hữu dụng)
Vậy phối hợp tối ưu là 46 sản phẩm X và 11 sản phẩm Y. Phối hợp này đạt tổng hữu dụng cao nhất là 484 đơn vị hữu dụng
Câu 4:
Khi thu nhập tăng lên đến 1220, các yếu tố khác không đổi, để tìm phối hợp tối ưu ta chỉ cần thay đổi thu nhập trong việc xây dựng PT đường ngân sách và giải hệ phương trình theo phương pháp giống câu 3. Cụ thể, ta có hệ phương trình
1220 = 10*X + 40*Y (1’)
và Y*40 = (X-2)*10 (2’)
ó
122 = X + 4Y (1’’)
và 2 = X – 4Y (2’’)
Lấy (2’’) + (1’’)
=> 2 X = 124 ó X = 62
Thế vào (2’’) => Y = 15
Thế giá trị X, Y vào hàm tổng hữu dụng ta được
TU = (62 – 2)*15 = 900 (đơn vị hữu dụng)
Vậy phối hợp tối ưu với ngân sách mới là 60 sản phẩm X và 15 sản phẩm Y. Phối hợp này đạt tổng hữu dụng cao nhất là 900 đơn vị hữu dụng
Câu 5:
Khi thu nhập tăng lên đến 1220, các yếu tố khác không đổi, lý luận tương tự câu 4 ta được hệ phương trình
740 = 10*X + 40*Y (1’)
và Y*40 = (X-2)*10 (2’)
ó
74 = X + 4Y (1’’)
và 2 = X – 4Y (2’’)
Lấy (2’’) + (1’’)
=> 2 X = 76 ó X = 38
Thế vào (2’’) => Y = 9
Thế giá trị X, Y vào hàm tổng hữu dụng ta được
TU = (38 – 2)*9 = 324 (đơn vị hữu dụng)
Vậy phối hợp tối ưu với ngân sách mới là 38 sản phẩm X và 9 sản phẩm Y. Phối hợp này đạt tổng hữu dụng cao nhất là 324 đơn vị hữu dụng
Câu 6
Xem đồ thị
Câu 7:
Ta có công thức tính hệ số co giãn của cầu theo thu nhập
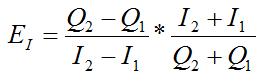
Tại mức thu nhập 720, ta tính được lượng cầu hàng hóa X là 38 (câu 5)
Tại mức thu nhập 900, ta tính được lượng cầu hàng hóa X là 46 (câu 3)
Thay các giá trị thu nhập và lượng cầu hàng hóa X trong khoảng thu nhập 720 đến 900, ta được
EI = [(46-38)*(900+720)]/[(900-720)*(46+38) = 0,86
Tại mức thu nhập 900, ta tính được lượng cầu hàng hóa X là 46 (câu 3)
Tại mức thu nhập 1220, ta tính được lượng cầu hàng hóa X là 62 (câu 4)
Thay các giá trị thu nhập và lượng cầu hàng hóa X trong khoảng thu nhập 900 đến 1220, ta được
EI = [(62-46)*(1220+900)]/[(1220-900)*(62+46)= 0,98
|